Teksti: Lasse Eronen, matematiikan pedagogiikan yliopistotutkija, Itä-Suomen yliopisto
Teksti on julkaistu alunperin Dimension verkkolehdessä 7.10.2019.
Kansikuva: Rawpixel (roungroat)
Arviointi on matematiikan harrastamisen kannalta keskeinen aktiviteetti, joka osaltaan on ollut mahdollistamassa nykymuotoisen matematiikan kehittymisen. Matematiikan kannalta arviointi tulee kuitenkin nähdä enemmän matemaattisen ajatteluprosessin osana kuin ajatteluprosessin onnistumista mittaavana aktiviteettina.
Puhun matematiikan harrastamisesta sen opiskelun tai oppimisen sijaan, sillä hyvä harrastus on vapaaehtoista ja sitä harrastetaan sen tuottamien tunnekokemuksien kuten, mielihyvän, jännityksen, löytämisen riemun tai vaikkapa oppimisen ilon vuoksi. Siinä missä joukkuelajien harrastamien tai vaikkapa kirjallisuus, myös matematiikka tarjoaa harrastajalleen edellä kuvattuja tunne-elämyksiä lukuisten muitten tunne-elämyksien lisäksi. Kuinka hienoa olisikaan, jos koulu voisi tarjota oppilaille tien löytää matematiikka harrastuksena ja itsessään matematiikka-ahdistusta heijastelevat ”olen aina ollut huono matematiikassa” – tyyppiset, omaa osaamista arvioivat sanaparret vähentyisivät käytäväkeskusteluissa!
Arviointi ollut kuumaperuna koulukontekstissa jo useamman vuoden. On puhuttu paljon muun muassa formatiivisen arvioinnin merkityksestä oppijan tietoisuuden kehittäjänä, oman oppimisen haltuunotossa ja toiminnan itsesäätelyn parantajana. Meneillään on useita kansallisia koulutus- ja kehittämishankkeita, joista kansallinen KAARO (Kaaro.fi) paneutuu arvioinnin kehittämistyöhön. Tässä hankkeessa oma toimintani keskittyy itsearvioinnin monipuolistamiseen erityisesti matematiikan opiskelussa. Vastaavasti LUMATIKKA (lumatikka.luma.fi), joka on matematiikkaa opettaville suunnattu täydennyskoulutushanke, on vienyt minut pohtimaan arviointia lukiotasolla ja tarjonnut mielenkiintoisia keskusteluja lukio-opettajien kanssa. Näissä koulutuksissa olemme päässeet pohtimaan arvioinnin merkitystä lukiomatematiikassa varsin monipuolisesti.
Lumatikka koulutusta suunnitellessa on mieleeni tullut professori Bernd Zimmermannin vuosikymmeniä kestänyt työ matematiikan historian parissa. Hänen tavoitteenaan oli ymmärtää matematiikan syntyprosessia tai oikeammin sitä miksi matematiikka on kehittynyt. Vuonna 2003 hän julkaisi artikkelin matematiikan kehittymiseen johtaneista motivaatioista, sekä kahdeksasta aktiviteettista, jotka hänen mukaansa ovat toisaalta vaadittu ja toisaalta riittäneet nykymuotoisen matematiikan kehittymiseen (Kuva 1). Zimmermannin mukaan matematiikka kehittyy näitten aktiviteettien verkossa ja näin ollen matematiikan monipuolinen harrastaminen edellyttäisikin tilanteita, joissa näitä aktiviteetteja tulisi käytetyksi monipuolisesti.
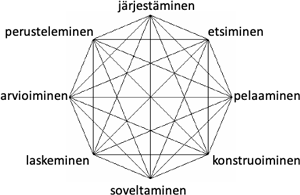
Yksi aktiviteettiverkon aktiviteeteista on arviointi. Tämä aktiviteetti täytyy kuitenkin ymmärtää hivenen arkimerkitystään laajemmin. Sen lisäksi, että arviointi on matematiikkaharrastajalle keskeinen aktiviteetti tulosten ja päätelmien oikeellisuuden arvioinnissa, arvioinnin aktiviteetti pitää sisällään myös yhteisöllisen arvottamisen ja sen, miten kautta historian erilaiset vallassa olleet mahdit ovat määrittäneet suotavan matematiikan harrastamisen sisällöt. Esimerkkinä mainittakoon Galilein eristäminen tiedeyhteisöstä esitettyään poikkeavia laskelmia vallalla olleeseen käsitykseen maailmankaikkeuden maapallokeskeisyydestä. Toisaalta tällainen arvottamisen aktiviteetti näyttäytyy myös nykypäivässä, esimerkiksi jos tarkastellaan sitä, miten eri valtaa pitävät tahot tahtovat tulkita (ja rahoittaa) vaikkapa erilaisia ilmaston lämpenemistä ennustavia matemaattisia malleja.
Arviointi lukiomatematiikan aktiviteettina
Entäpä, jos lukiomatematiikan opetuksessa arviointia tarkasteltaisiinkin matematiikan harjoittamisen aktiviteettinä. Miten järjestää oppilaille sellaisia matematiikan harrastamisen tilanteita, joissa heidän arviointitaitonsa kehittyisivät siten, että ne palvelisivat vahvasti myös matematiikan harjoittamista?
Yksi keskusteluissa esiinnoussut näkökulma oli ratkaistavaksi valittujen tehtävien valitseminen. Opettajien kokemuksen mukaan näyttää siltä, että varsin monesti oppilaat ottavat tarkasteluun tehtävän joko numerojärjestyksessä tai muutoin sattumanvaraisesti. Oppilaitten olisikin hyvä tarkastella tehtävien tekemistä siitä realiteetista, ettei aika todellisuudessa tule riittämään kaikkien tarjolla olevien tehtävien tekemiseen, vaan jokainen tehtävä on valintatilanne. Kun valitsen tämän tehtävän tulen samalla valitsemaan pois joukon muita tehtäviä koska aikaresurssini on rajallinen. Miksi juuri tämän tehtävän tekeminen on minulle tärkeää? Pohdimme kurssilla keinoja tämän valinnan korostamiseksi. Toimisiko tässä käänteinen ajattelu siten, että oppilaille tarjottaisiin kokemus tilanteesta, heillä olisi käytössään maksimäärä tehtäviä tai aikaa, jossa tällä kokeilujaksolla tulisi matematiikka opiskella?
Toisekseen arviointitaitoa ja samalla matematiikan kirjoittamisen taitoa voi kehittää ns. ”what went wrong” -tehtävätyypeillä, joissa oppilas arvioi jo jonkin toisen valmiiksi tuottaman ratkaisun oikeellisuutta ja perustelun riittävyyttä. Monet Lumatikka-koulutukseen osallistuneista opettajista käyttivät hyväkseen täysin anonymisoituina esim. aikaisemman preliminäärikokeen tehtävien vastauksia laittaen tehtävän ratkaisuja kurssin oppilasryhmien pohdittavaksi. Tällöin oppilasryhmien (2–3 oppilasta) tehtävänä oli tarkastella ratkaisun oikeellisuutta ja perustelujen riittävyyttä.
What Went Wrong -tehtäväesimerkki MAA7 kurssilta
Kiitokset seuraavan tehtävän tehtävämateriaalista kuuluvat Itä-Suomen harjoittelukoulun opettajalle Kalle Ventolalle.

Kokemuksia tehtävätyypistä
Ohessa muutaman tätä tehtävätyyppiä kokeilleen opettajan raportoimia oppilaskokemuksia:
”Opiskelijoiden loppukommenttina tehtävän annosta oli, että se oli ihan mielenkiintoinen ja toki muulloinkin voisi tehdä vastaavaa harjoittelua ryhmissä. Eräs opiskelija totesi havainneensa omat virheet ja puutteet suorituksissaan, oli kuitenkin siihen tyytyväinen ja koki oppineensa merkintöjen tärkeyden.”
”Opiskelijoiden kokemuksen mukaan tämä jälkimmäinen arviointivaihe osoittautui jopa ratkaisuvaihetta huomattavasti opettavaisemmaksi. Opiskelijat huomasivat, mihin muistisääntöjä voi hyödyntää ja erityisesti, että matematiikalla saatiin tehtävä helpommaksi”
”Opiskelijat olivat hyvin tyytyväisiä ja motivoituneita tehtävään, toisten virheiden etsiminen ja korjaaminen oli hyvin opettavaista. Keskustelu oli aktiivista ja oppilaat innostuneita, joten olin tyytyväinen.”
”Keskustelu oli vilkasta ja opiskelijat kommentoivat jälkeenpäin, että olisi hyvä, jos vastaavia tehtäviä olisi jokaisella kurssilla. ”Näkisi, että voi tehdä monella eri tavalla” ja ”huomaa helpommin, missä itsekin voi parantaa” olivat yleisimmät kommentit.”
Oppilailta kerätty palaute tehtävätyypistä on ollut varsin positiivista ja se on otettu silmiä avaavana kokemuksena. Näyttääkin siltä, että tehtyjen ratkaisujen arviointi ja arvottaminen ovat varsin kehittävää ja matematiikan opetukseen keskeisesti kuuluvaa toimintaa. Sitä voi käyttää osana myös oppilaan oman matemaattisen identiteetin kehittämistä ja siinä toteutettavaa itsearviointia. Tästä kertominen puolestaan vaatii oman tilan ja ajan. Lumatikka-hankkeella on muuten täysin avoimet mooc-kurssit (ks. lumatikka.luma.fi), joihin tutustumalla pääset osalliseksi tästä kaikesta keskustelusta. Tervetuloa!
[1] Zimmermann, B. 2003. On the genesis of mathematics and mathematical thinking – a network of motives and activities drawn from the history of mathematics. Teoksessa L. Haapasalo & K. Sormunen (toim.) Towards Meaningful Mathematics and Science Education. Joensuun yliopiston kasvatustieteiden tiedekunnan selosteita 86, 29-47.

